Не так уж и много людей подсчитывают в уме большие числа. Да и зачем, если всегда под рукой телефоны со встроенными калькуляторами? Но гаджет может разрядиться или дать сбой, а вот ваша голова всегда с вами. Но даже если нет насущной необходимости в устных подсчетах, вы можете использовать их в качестве свое рода «физкультуры» для мозга.
Сложение
Чтобы посчитать сумму даже самых больших чисел, для начала надо научиться безошибочно суммировать другие числа с 10.
Прием «опоры на десяток» заключается в том, что надо посмотреть: сколько единиц не достает самому большому слагаемому до 10? И затем прибавить необходимое число единиц.
Например, нужно сложить 8 и 5. Восьмерке до десятки не хватает двух единиц. Тогда от пятерки надо будет отнять два:
8 + 5 = (8+2) + (5-2) = 10 + 3 = 13
А можно поступить еще проще. Подставляем вместо восьмерки десятку и не забываем отнять двойку от полученной суммы:
8 + 5 = 10 + 5 – 2 = 15 – 2 = 13
Чтобы суммировать сложные числа, надо разделить их на разрядные части и суммировать их между собой.
Допустим, надо сложить 325 и 426. 325 распишем как 300 + 20 + 5. Соответственно, 426 = 400 + 20 + 6. Теперь суммировать будет проще:
325 + 426 = (300+400) + (20+20) + (5+6) = 700 + 40 + 11 = 751
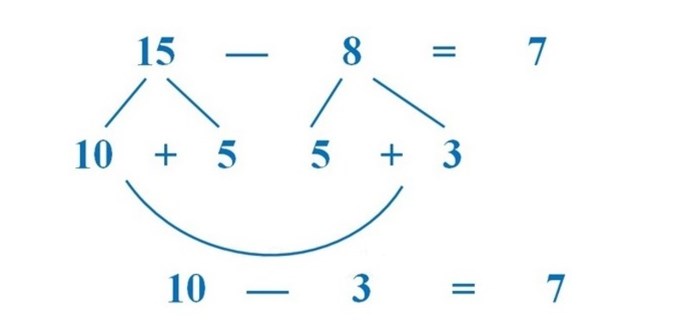
Вычитание
При вычитании мы тоже облегчаем подсчет с помощью разбивания чисел на разрядные части. Но в данном случае мы делаем это только с тем числом, которое вычитаем.
Например, надо из 876 вычесть 325.
325 = 300 + 20 + 5
876 – 325 = 876 – 300 – 20 – 5 = 576 – 20 – 5 = 556 – 5 = 551
Упражняясь, старайтесь не расписывать весь этот алгоритм на бумаге, а визуализировать и считать в уме.
Умножение
Умножение – это повторение числа заданное количество раз. Например, если 8 надо умножить на 5, это значит, что надо сложить вместе пять семерок:
8 х 5 = 8 + 8 + 8 + 8 + 8 = 40
Сложные задачи разбиваются на простые. Поэтому чтобы быть способными умножать сложные числа, необходимо выучить таблицу умножения. Без этого дальнейшие действия невозможны.
Умножение многозначных чисел на однозначные
Допустим, нам надо умножить 376 на 5. Разобьем 376 на разряды, перемножим каждое полученное число на 5, затем суммируем результаты:
376 = 300 + 70 + 6
376 х 5 = 300х5 + 70х5 + 6х5 = 1500 + 350 + 30 = 1880
Умножение двузначных чисел
Чтобы умножить одно двузначное число на другое, надо оба числа разбить на разрядные части. Например, надо умножить 56 на 48:
56 х 48 = 56 х (40 + 8) = 56 х 40 + 56 х 8 = 50х40 + 6х40 + 50х8 + 6х8 = 2000 + 240 + 400 + 48 = 2688
И еще один способ. Умножим 54 на 39. Сделаем это в несколько действий: сначала умножим 54 на 30, затем 54 на 9 и суммируем результаты:
- 54 х 30 = (50+4) х 30 = 1500 + 120 = 1620
- 54 х 9 = (50+4) х 9 = 450 + 36 = 486
- 1620 + 486 = 2106

Как умножить на 11
Есть один прием. Для этого надо сложить две цифры числа, и получившуюся сумму поместить между цифрами изначального числа. Это и есть результат умножения заданного двузначного числа на 11.
Внимание: прием работает, если сумма цифр, из которого состоит двузначное число, меньше 10!
Умножим 43 на 11:
4 + 3 = 7 (меньше 10)
473
43 х 11 = 473
А теперь попробуем использовать это метод при умножении 68 на 11:
6 + 8 = 14 (больше 10)
6148
68 х 11 = 748
Возведение в квадрат
Теперь познакомимся с приемом, благодаря которому можно возводить двузначные числа в квадрат.
Внимание: этот прием работает только с числами, оканчивающимися на 5!
Вот суть приема. Сначала надо умножить первую цифру двузначного числа на следующую за ней. Например, надо возвести в квадрат число 65. Первая цифра этого числа – 6. За шестеркой следует семерка. Поэтому умножаем 6 на 7 и получаем 42. Это первая часть нашего результата.
Чтобы получить вторую часть, надо вторую цифру двузначного числа умножить на саму себя, то есть пятерку надо умножить на пятерку (возвести в квадрат). Получаем 25.
Таким образом:
652:
6 х 7 = 42
5 х 5 = 25
Получается 4225
652 = 4225
Попробуем произвести те же действия с числом, заканчивающимся не на 5. Например, 72.
7 х 8 = 56
2 х 2 = 4
564
722=5184

Деление чисел
По умолчанию имеется ввиду, что все владеют таблицей умножения, и проблем с делением чисел меньше 100 нет.
Деление на однозначное число
При делении многозначных чисел на однозначное надо выявить наибольшую часть, которая делится в соответствии с таблицей умножения.
Допустим, надо разделить 7335 на 9. Согласно таблице умножения, ближайшее число, которое делится на 9, это 7200. Распишем:
7335 : 9 = (7200+135) : 9 = 800 + 135:9
Мы получили число от первого деления – это 800.
Теперь из числа 135 выявляем максимальное число таблицы, которое делится на 9. Это 90.
135:9 = (90 + 45) : 9 = 10 + 45:9
Второе число – 10.
Осталось выполнить последнее деление и сложить все полученные результаты:
45:9 = 5 – третье число.
Таким образом:
7335 : 9 = 800 + 10 +5 = 815

Деление на двузначное число
При делении на двузначное число надо вспомнить о «правиле последней цифры» при умножении двух чисел.
Иными словами, если мы умножаем, например, 27 на 325, то результат наших действий будет заканчивать на 5, потому что 7 х 5 = 35. И действительно, 27 х 325 = 8775.
Теперь вернемся к делению. Например, нам надо разделить 2394 на 42.
Начинаем с метода «научного тыка»: вспоминаем таблицу умножения и пытаемся подобрать самое близкое число, которое даст 2394 при умножении на 42. Для нас это 50.
42 х 50 = 2100
Значит, нужное число больше 50 и меньше 60, потому что если 60 умножить 42, будет явно больше 2400 (а именно 2520).
Теперь надо определить последнюю цифру искомого числа. Ее умножение на 2 (последнюю цифру числа 42) должно давать конечную цифру 4. Судя по таблице умножения, сюда подходят цифры 2 и 7, то есть наше искомое число – 52 или 57. Проверяем:
52 х 42 = 2184
57 х 42 = 2394
Правильный вариант – 57.
Пара полезных советов
- старайтесь тренироваться в счете каждый день;
- можно установить приложение, чтобы не придумывать себе задачки – это сэкономит вам время и силы;
- читайте специализированные книги – из них вы сможете узнать о других приемах устного счета.